On Gerrymandering

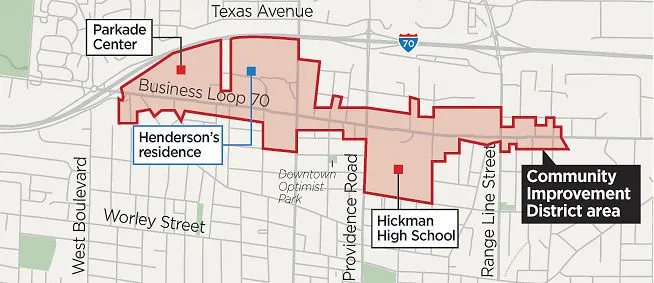
There’s been a lot of talk about a recent gerrymandering disaster in Missouri. For the best discussion, read Lowering the Bar’s take on it. Coincidentally, I reviewed an article by Jeff Suzuki for Mathematical Reviews over the weekend, on how gerrymandering can lead to stable results, even amongst minority views:

Suzuki provides a discussion of the optimal strategy for packing election districts. His analysis begins with a discussion of existing election districts and an analysis of how certain gerrymandering efforts can work against their intended beneficiaries, presumed to be the political party making the decision. From this analysis, Suzuki finds the optimal strategy for packing electoral districts based on two parties and allowing for different levels of voter commitment. Based on this analysis and strategy, the author finds extreme candidates can be elected and reëlected, even when their position is further from the median voter than should be expected under the median voter theorem.

Suzuki, Jeff, The self-limiting partisan gerrymander: an optimization approach, College Math. J. 45 (2014), no. 5, 338–348.

Jeff Suzuki also wrote Constititional Calculus, which I also reviewed for MR, last month.

Image by the Columbia Tribune.