You're out of order! The whole operation's out of order!
Wednesday October 07, 2015


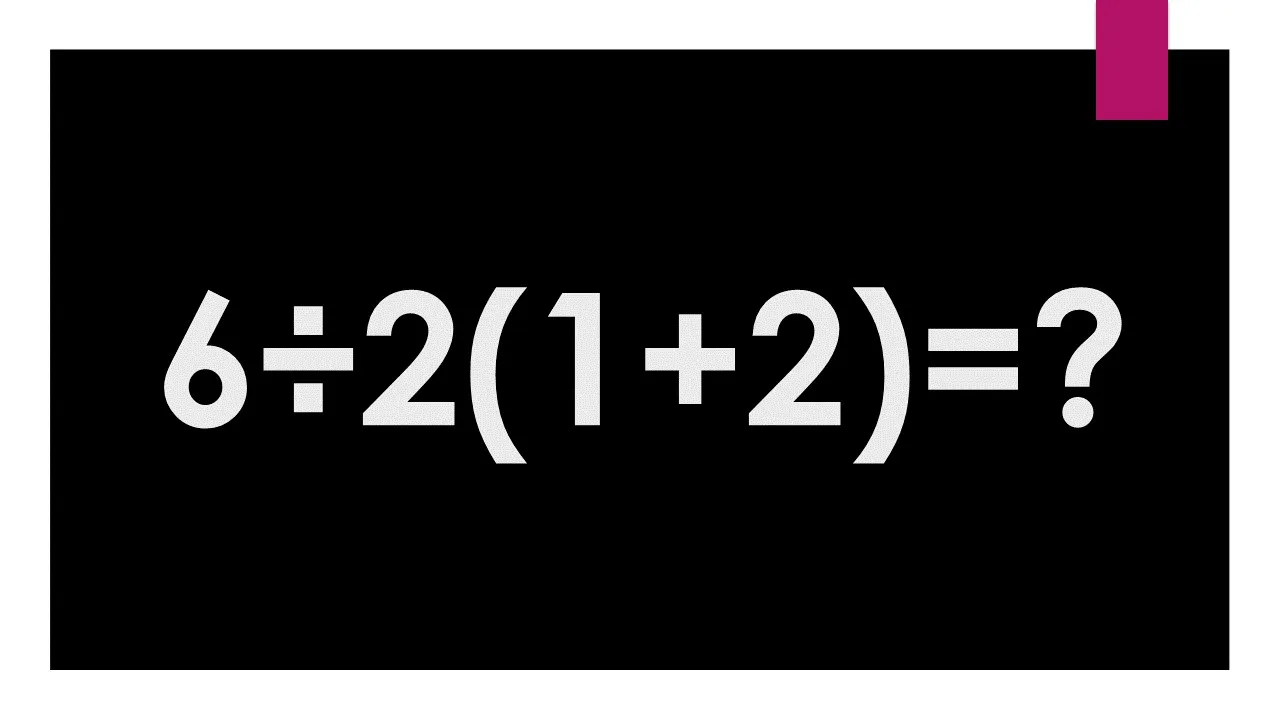
It’s ambiguous. There are two problems here. First, PEMDAS doesn’t necessarily include all of the things in this example problem. The implicit multiplication is one. That is, which rule governs 2(? Some argue it is covered by the parenthesis rule. Others the multiplication rule. When pressed, many mathematicians resolve the ambiguity by introducing a new rule that places implicit multiplication ahead of explicit. But others, who really fail to understand PEMDAS, argue implicit multiplication is the same as explicit. This is not obviously incorrect, but neither is it obviously correct. That’s why these two calculators give different answers.

The second problem is inline division. Because it can introduce these sorts of questions, many publishers define inline division as lower precedence than explicit multiplication and division. Lets be clear, you can cite PEMDAS, but given how many different versions there are, you may not be helping your case. Generally, pushing down inline division resolves the ambiguity here, but I imagine a carefully crafted example could break it, too.
The implicit rules and inline division really come to a head in the example,
This is clearly the same as [latex]4 / (4 - 2 * 2) = 4 / (4 - 4) = 4 / 0 = \text{undefined}[/latex]. But if you run PEMDAS over it naïvely, you get [latex] 4 / 4 - 2 * 2 = 1 - 4 = -3 [/latex], which is really, really, wrong. But I think the implicit division rule is much clearer, in this example, than the implicit multiplication rule in the source problem.
Slate wrote up this problem a couple of years ago. That article makes a critical point, PEMDAS isn’t a rule. It’s a convention. There’s nothing absolute about it, like there is true mathematical rules. It’s just the method we adopt to ensure we communicate mathematics effectively. The first of those, that parentheses are operated on first, is ignored in this example. Because, of all the implicit rules in PEMDAS, the most important is use parentheses to eliminate ambiguity.
Image lifted from Yo Amo Las Matemáticas y Las Ciencias / YouTube.